1. はじめに

前回から、オプション・プライシングへのモンテカルロ・シミュレーションの利用法をご紹介しています。 オプション・プライシングへのシミュレーションの利用は、そもそも何でシミュレーションをする必要があるのかの理解が難しいので、前回はその辺りを説明いたしました。

今回からは、より具体的な考え方と計算方法について見ていきます。 前回同様、今回もある程度オプション理論などを勉強された方でないと意味不明な箇所が多くなってしまうかもしれなせんが、 そのような方も、とりあえずご参考として最後までお読みいただけると幸甚です。

　2. 前提となる価格変化モデル

オプションのプライシングにおいては、プライシングの前提として、原資産の価格変化について、何らかの「モデル」を仮定する必要があります。このモデルに従って原資産が価格変化していくという前提に立った上で、オプションと同じキャッシュフローを発生させるポートフォリオ構築を考え、そのポートフォリオ構築に必要な金額が（無裁定理論より）オプションの価格だ・・というのがオプション価格計算の本質です。

しかし、前回お話したように、複製原理に基づく価格計算は、オプションの場合一般には難しいです。 このため、金融工学の原理を使い、リスク中立経済下において、前提としたモデルに従い原資産が価格変化する場合の、満期時オプション価値の期待値を求め、その現在価値を求めるわけです。

よって、オプション価値というものは、前提とする原資産価格変化のモデルによっても変わってきます。

ブラック・ショールズ式も、原資産の価格変化について一定の仮定（モデル）を置いた上での式なわけですが、そのモデルは以下のようなものです（通常は「確率微分方程式」と呼ばれる難しい式の形でモデルを定義しますが、ここではより分かり易い形でモデル式を立てることとします）。

今後のシミュレーションもこのモデル式に基づき行います。

　■ ＢＳモデルで前提とする、原資産の価格変化モデル式

説明しましょう。 S というのはオプションの対象である原資産のことであり、 S0 というのは原資産の現在価格を、 ST というのは、オプションの満期である時点 Ｔ における価格を表しています。

e というのは、数学で以下のように定義される特殊な数です。

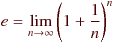
具体的な値としては、
　
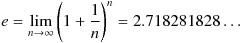
といった値を取ります。表記した部分だけだと、以下 1828 が繰り返し続きそうですが、実際はこのあと規則性なく数字がずっと並びます。π（円周率）と同じタイプの値です。 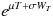というのは、この e という値の 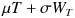乗ということです。この辺りも、理系の方などで e という値についてよく知っている方や、ファインナンス理論の連続複利という概念を知っている方でないと理解は難しいと思います。

ここで頭が「？」となってしまった方のために、この式の直観的なイメージを申し上げておくと、 例えば er という値を考えると、この式は基本的には以下のような計算をしていることになります。
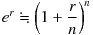　 　（ただし n は非常に大きい数）

式の右側は、「期間１年、金利 r 、年 n 回複利」の預金に元本１円を預け入れた場合の満期時元利合計額を表しています。 ただ、正確には er という値は、この式において n を限りなく大きくしていった場合にこの式の値が収束する値を意味します。 つまり、 n を 365 （１日複利の場合）や 31536000 （１秒複利の場合）などにしていけば、ほぼ er に近い値が得られることになります。

よって「 ｎ は非常に大きい数」と条件付けた上で、右辺とほぼイコールとしているわけです。 この er で表される、限りなく複利回数を多くした場合の複利運用を「連続複利」と呼んでいます。

ですから、（１）式は、イメージ的には複利金利に相当する部分に 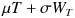という値が入っている式ということになります。そこで、次に説明すべきポイントはこの 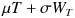という式がどんなことを表現しているか、ということです。