- Home >
- デュレーションってなんだろう >
- 第5回 債券投資の基本構造を理解する (その2)
●日本FP協会 継続教育対象講座●
β値やデュレーションなど、実務に役立つ知識をしっかり学べる
債券・株式・ポートフォリオ入門コース

デュレーションってなんだろう
第5回 債券投資の基本構造を理解する (その2)
3. 投資期間が短い場合の債券投資収益率の考え方
それでは、まず債券投資の期間が短い場合を考えてみましょう。
短いと言っても、正確に言うと、ここでいう短期間の投資とは、償還日よりずっと前の時点で売却してしまい、かつ投資期間が1年以内ぐらいの期間の投資というものを想定しています。期間そのものは短くても償還日まで投資する場合は、次に延べる投資期間が長い場合の考え方があてはまりますので、その点ご注意ください。
今、瞬間的にある債券の利回りが変動し、それにより価格が変化するという場合ならば、 すでに学習した「修正デュレーション」を使って
債券投資収益率 ≒ -利回り変化 × 修正デュレーション
とすればよいことは、すでにおかわりいただけたと思います。
しかし、短期といっても、通常は多少時間が経過することが多いでしょう。そして、債券というものは、利回りが変化せずとも時間が経てば価格は変化し、収益が発生するものです。従って、上の式以外に「時間の経過により発生する収益」を考慮しなければなりません。
では、「利回りは変化しないが時間が経過した」場合の債券投資収益率はいくらになるでしょうか? クーポンの再運用レートを考慮しなくてよい期間であれば、これは現状の利回り(複利利回り)になります(クーポンの再運用収入が問題になるケースでも、クーポンの再運用レートと現在の利回りが一致すれば、「債券投資収益率=現状の利回り」となります)。
それでは、現在の利回り r 、修正デュレーション
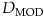 の債券に、ある程度の投資期間(時間の経過による収益率が問題にならないほど短いわけではないが、クーポンの再運用収入が問題になるほどではない期間)
の債券に、ある程度の投資期間(時間の経過による収益率が問題にならないほど短いわけではないが、クーポンの再運用収入が問題になるほどではない期間)
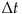 だけ投資し、投資終了時点までに利回りが
だけ投資し、投資終了時点までに利回りが
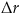 だけ変化したという場合の投資収益を式で表現してみましょう。
だけ変化したという場合の投資収益を式で表現してみましょう。
クーポンの再運用収入が問題にならないのであれば、この債券の利回りが、いつ
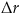 だけ変化したとしても、債券収益率に変化は無いはずですから、仮に、債券購入後、利回りが、rから
だけ変化したとしても、債券収益率に変化は無いはずですから、仮に、債券購入後、利回りが、rから
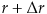 へ瞬時に変化し、その後、利回り
へ瞬時に変化し、その後、利回り
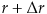 のまま
のまま
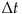 だけ時間が経過したとします。すると、
だけ時間が経過したとします。すると、
債券投資収益率
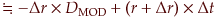 …… (1)式
…… (1)式
と表現できることになります。(
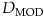 :修正デュレーション)
:修正デュレーション)
これが、「あまり投資期間が長く無い場合」の債券投資収益率の構造を示す式です。
具体的に (1) 式を使って計算してみましょう。
例えば、修正デュレーションが 4.7 という値で、現在利回り 0.5% の債券に半年間(0.5年間)投資することを考えましょう。
その間に利回りが 0.2% 低下するというシナリオの元、半年間の収益率を計算してみると、
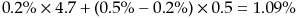
となります。
この式が合っているかどうかは、期間 5.0 年、クーポン 2.5 %(半年払い)、利回りが 0.5%(修正デュレーション:4.73)といった債券を前提に実際にこのケースにおける収益率を計算してみてください。もともと (1) 式は債券の投資収益率を近似的に表現する式なので、そんなにピッタリというわけには行きませんが、大体合っていることが確認できるはずです。
ところで、この計算例からも推測できると思いますが、(1) 式で投資収益率が近似的に表現できるような 短期間の債券投資の場合においては、一般論として、基本的に利回りが変化して価格が変化することによって収益が大きく変わる ということがわかります。
今の計算例でも、利回りが 0.5% の債券に投資したのに、収益率が約 1% 強ぐらいの収益率になった原因は、 (1) 式の中でも 0.2%×4.7 という、「利回り変化×修正デュレーション」という計算が表現している部分の影響が大きいわけです。 したがって、短期間の債券投資でも、その間の利回り変化が結構大きい場合は、予想以上に高い収益率になったり、低い収益率になったりするわけです。
著作権・免責事項
- 「やさしい金融エンジニアリング講座」(以下、本解説集)の文章、図表などの著作権は、シグマベイスキャピタル株式会社に帰属しますので、複製・転載・引用・配布などは一切禁止します。
- 本解説集の利用により生じた損害はいかなる理由であれ、一切責任を負いかねますので予めご了承下さい。
- 本解説集は、予告なしに内容が変更・削除等されることがあります。
- 内容に対するご質問にはお答えすることはできませんので、ご了承下さい。
●日本FP協会 継続教育対象講座●
相場の知恵の結晶、奥深いテクニカル分析を基礎から学ぶ!
【eラーニング】テクニカル分析 初級コース





